معادلات دیفرانسیلی چه هستند؟
معادلات دیفرانسیل جزیی میتواند همه چیز را از حرکت سیارات تا حرکت تکتونیک صفحهای را توصیف کنند، اما حل این معادلات بسیار دشوار است. برای افراد معمولی این معادلات اهمیت چندانی ندارند. اما برای فیزیکدانان و مهندسین این معادلات از اهمیت بسیاری برخوردار هستند.
معادلات دیفرانسیل جزئی یا PDE ها به نوعی شبیه معجزه هستند. این معادلات در توصیف زمان و مکان واقعا خوب عمل میکنند. همچنین برای توصیف پدیدههای فیزیکی در جهان بسیار مفید هستند. معادلات دیفرانسیل جزئی میتوانند برای مدلسازی همه چیز از مدارهای سیارهای تا لایههای زمینی و حرکت تودههای هوایی مورد استفاده قرار گیرند.

از طرفی این معادلات امکان پیش بینی فعالیتهای لرزهای زمین و طراحی ایمن هواپیما را به ما میدهند.
حل معادلات دیفرانسیل جزئی
حل PDEها بسیار دشوار است. تصور کنید قصد دارید برای طراحی یک هواپیمای ایمن، تودههای هوایی را شبیه سازی کنید. PDEهای شناخته شدهای به نام Navier-Stokes وجود دارد، که برای توصیف حرکات هوا استفاده میشوند. حل Navier-Stokes به ما تصویری از حرکت تودههای هوایی در هر لحظه را میدهد.
این محاسبات بسیار پیچیده و فشرده هستند. به همین دلیل رشتههایی که از PDE های زیادی استفاده میکنند اغلب برای انجام ریاضیات به ابَر کامپیوترها اعتماد میکنند. به دلیل سختی حل این معادلات، هوش مصنوعی، علاقه خاصی به این عرصه نشان داده است. میتوان برای تسریع در روند حل این معادلات از یادگیری عمیق استفاده کرد. موفقیت این روند در موفقیت تحقیق و مهندسی بسیار مفید است.
کاربرد یادگیری عمیق در حل معادلات
اکنون محققان در Caltech یک روش جدید برای یادگیری عمیق برای حل PDE ارائه دادهاند که کاملاً دقیقتر از روشهای یادگیری عمیقی است که قبلاً توسعه یافتهاند. همچنین بسیار تعمیم پذیرتر است.

این روش قادر به حل کامل خانوادههای PDE – مانند معادله Navier-Stokes برای هر نوع سیالی – بدون نیاز به آموزش مجدد است. همچنین 1000 برابر سریعتر از فرمولهای ریاضی سنتی است، که باعث افزایش اعتماد ما به ابر رایانه ها و افزایش توانایی محاسباتی ما برای مدل سازی مشکلات حتی بزرگتر می شود.
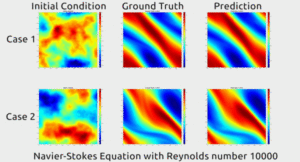
قبل از اینکه به چگونگی انجام این کار توسط محققان بپردازیم، اجازه دهید ابتدا نتایج را ارزیابی کنیم. در تصویر زیر، شواهد چشمگیری را مشاهده می کنید. ستون اول دو عکس فوری از حرکت سیال را نشان می دهد. ستون دوم نشان می دهد که چگونه سیالات در زندگی واقعی حرکت می کنند. ستون سوم نشان می دهد که چگونه شبکه عصبی حرکت سیال را پیش بینی کرده است. در اصل ستون دوم و سوم یکی هستند.
کاربرد شبکههای عصبی مصنوعی در حل معادلات
اولین چیزی که باید در اینجا فهمید آن است که شبکههای عصبی اساساً توابع تقریب زننده هستند. منظور این است که وقتی آنها در حال آموزش روی مجموعه دادههایی از ورودیها و خروجیها هستند، در واقع در حال محاسبه عملکرد یا مجموعه ای از عملیات ریاضی برای ربط ورودیها به خروجیها هستند.
یک شبکه عصبی تشخیص دهنده “گربه” را تصور کنید. به این شبکه عصبی تعداد زیادی از عکس میدهید. برخی از این عکسها تصویر گربه هستند و برخی دیگر عکسهایی از چیزهای دیگر هستند. هر گروه را به ترتیب با 1 یا 0 برچسب گذاری میکنیم (خروجی). شبکه عصبی هر تصویری که گربه است را با 1 برچسب گذاری میکند و تصاویر دیگر را با صفر. به این ترتیب میتواند زمانی که یک تصویر جدید را دریافت کرد بگوید این تصویر گربه هست یا نه.

این فرایند تقریب عملکرد همان چیزی است که ما برای حل یک PDE نیاز داریم. ما در نهایت سعی در یافتن تابعی داریم که مثلاً حرکت ذرات هوا را در فضا و زمان فیزیکی به بهترین وجه توصیف کند.
شبکههای عصبی معمولاً برای تقریب توابع بین ورودی و خروجی تعریف شده در فضای اقلیدسی، با نمودار کلاسیکی با محورهای x،y و z آموزش داده میشوند. اما این بار، محققان تصمیم گرفتند ورودیها و خروجیها را در فضای فوریه، نوع خاصی از نمودار برای ترسیم فرکانس های موج، تعریف کنند.
به گفته آنیما آناندکومار ، استاد Caltech با همکارانش، استادان اندرو استوارت و کاوشیک، که نظارت بر این تحقیق را بر عهده داشت، شهودی که آنها از کار در زمینههای دیگر به دست آوردند این است که چیزی مانند حرکت هوا در واقع میتواند ترکیبی از فرکانس های موج باشد.
پیش بینی تودههای هوایی
جهت کلی باد در سطح کلان مانند یک فرکانس کم با امواج بسیار طولانی و سست است. در حالی که گردابهای کوچکی که در سطح میکرو تشکیل میشوند مانند فرکانسهای بالا با فرکانسهای بسیار کوتاه و سریع هستند.
چرا این مسئله مهم است؟
از آنجا که تقریب عملکرد فوریه در فضای فوریه بسیار راحت تر از درگیری با PDEها در فضای اقلیدسی است، کار شبکه عصبی را بسیار ساده می کند. مهمترین دستاورد شبکههای عصبی دقت و کارایی است. علاوه بر مزیت بسیار زیاد سرعت نسبت به روشهای سنتی، در هنگام حل Navier-Stokes ، تکنیک آنها نسبت به روشهای یادگیری عمیق ، 30٪ کمتر خطا دارد.
همه چیز بسیار هوشمندانه است و میتوان این روش را برای کاربردهای دیگر نیز تعمیم داد.
روشهای قبلی یادگیری عمیق باید به طور جداگانه برای هر نوع سیالی آموزش داده میشدند، در حالی که این روش فقط یکبار آموزش داده میشود. اگرچه محققان هنوز سعی نکرده اند این مورد را به سایر نمونه ها گسترش دهند، اما باید بتوانند هنگام حل PDE های مربوط به فعالیت لرزه ای، یا هر نوع ماده هنگام حل PDE های مربوط به رسانایی گرمایی، از ترکیبات زمین استفاده کنند.
شبیه سازی
اساتید و دانشجویان دکترا این تحقیق را فقط برای سرگرمی نظری انجام ندادند. آنها می خواهند هوش مصنوعی را به رشتههای علمی بیشتری برسانند. آناندکومار ابتدا از طریق گفتگو با همکاران مختلف در زمینه علوم آب و هوا زلزله شناسی و علوم مواد تصمیم گرفت با همکاران و دانشجویانش وارد چالش PDE شود. آنها اکنون در تلاشند تا روش خود را با محققان دیگر در Caltech و آزمایشگاه ملی لارنس برکلی عملی کنند. یک موضوع ویژه تحقیقاتی آناندکومار که در مورد آن هیجان زده است: تغییر اقلیم است.
Navier-Stokes فقط در مدل سازی حرکت تودههای هوا مهارت ندارد؛ همچنین برای مدل سازی الگوهای آب و هوایی استفاده میشود. وی میگوید: “داشتن پیشبینیهای خوب آب و هوایی در مقیاس جهانی، مشكلی چالش برانگیز است و حتی در بزرگترین ابر رایانه ها، امروز نمیتوانیم این كار را در مقیاس جهانی انجام دهیم. بنابراین اگر بتوانیم از این روشها برای سرعت بخشیدن به کل فرآیند استفاده کنیم، بسیار چشمگیر خواهد بود”.






